Definição de Euclides, Axiomas de Incidência e plano, e Espaço de Incidência
1. Origem da Geometria
A palavra “geometria” vem do grego geometrein (geo, “terra”, e metrein, “medida”); originalmente geometria era a ciência de medição da terra. O historiador Herodotus (século Va.C.), credita ao povo egípcio pelo início do estudo da geometria, porém outras civilizações antigas (babilônios, hindu e chineses) também possuiam muito conhecimento da geometria.
Um pouco de História da Geometria e da sua relação com outras áreas matemáticas, nomeadamente a Álgebra elementar, desde as origens heurísticas (egípcios e babilónicos), passando pelo desenvolvimento e sistematização durante o período helenístico (axiomática de Euclides) e cobrindo, a traços largos, desenvolvimentos posteriores (o problema das paralelas) até ao descobrimento das geometrias não-euclidianas no século XIX;Mas é sem dúvida com os geómetras gregos, começando com Tales de Mileto (c. 624--547 a.C.), que a geometria é estabelecida como teoria dedutiva. A intuição, a descoberta empírica e a experimentação têm o seu lugar, mas é o raciocínio dedutivo, a demonstração ou dedução a partir de hipóteses conhecidas que estabelece a veracidade das proposições geométricas.
Pitágoras (c. 572-497 a.C.), após longas viagens pela Babilónia e Egipto, estabeleceu-se em Crotona, cidade grega no sul da Itália, por volta de 530 a.C., onde fundou um culto religioso e filosófico que cultivava a purificação do espírito através da música e da matemática.
Arquimedes de Siracusa (287 – 212 a.C.) é o segundo grande matemático da chamada primeira escola de Alexandria. Os seus escritos são em regra concisos, mas plenos de originalidade. A sua obra prima é o tratado Da esfera e do cilindro contendo, entre outros, o célebre resultado de que a razão entre as áreas da superfície de uma esfera e de um cilindro no qual a esfera está inscrita é igual a , e é também igual à razão entre os respectivos volumes.
2. Definições de Euclides
Euclides nasceu por volta de 330 a.C. na Síria, mas foi em Atenas que desenvolveu seu trabalho com a matemática e, portanto, com a geometria. Apesar de não se ter muito conhecimento sobre sua trajectória existencial ele ficou conhecido como o “O pai da Geometria” em Alexandria, onde
atuou como professor de matemática (geometria e álgebra). Tudo o que sabemos sobre Euclides foi escrito muito depois de sua passagem pela Terra.
Essas civilizações antigas usavam a geometria principalmente para fins práticos e havia pouca ênfase no raciocínio por trás das declarações. Euclides pensava na geometria como um modelo abstrato do mundo. As ideias do ponto, linhas, formas foram derivadas do que foi visto no mundo real. Ele estudou objectos do mundo real para formalizar o conceito de sólido. Portanto as definições de Euclides são:
- Um ponto é aquele que não tem parte;
- Uma linha tem menos largura;
- As extremidades de uma linha são pontos;
- Uma linha reta é uma linha que se encontra uniformemente com os pontos sobre si mesma;
- Uma superfície é aquela que tem comprimento e largura apenas;
- As bordas de uma superfície são linhas; e
- Uma superfície plana é uma superfície que se encontra uniformemente com linhas rectas sobre si mesma.
3. Axiomas
3.1. Axiomas de incidência
Um axioma é um conceito matemático que não precisa de demonstração para ser verdadeiro. É uma ideia considerada óbvia e tomada como consenso, mesmo sem provas para tal. Os axiomas servem como base para a dedução de outras verdades.
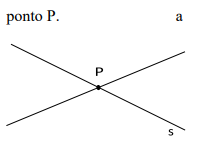
Axiomas de incidência definem a ideia expressa pela noção de estar em, além de estabelecer uma conexão entre os termos primitivos do plano: ponto e reta. Exemplo: Rectas r e a concorrentes no
ponto P.
3.2. Axiomas de Ordem
Os axiomas de ordem definem a ideia expressa pelo termo estar entre, e tornam possível, com base nessa ideia, descrever uma ordem de sequência dos pontos sobre uma reta. Os pontos de uma reta têm uma certa relação um com o outro, e a noção de estar entre servirá para descrevê-la.
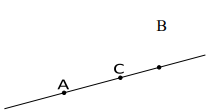
Exemplo: O ponto C está entre A e B
3.3. Axiomas sobre Medição de Segmento
O conceito de medida de um segmento é introduzido mediante a adoção de uma unidade de comprimento que, neste faremos axiomaticamente. Uma vez que soubermos medir segmentos estaremos aptos a poder compará-los em tamanho. A cada segmento AB está associado um único número real positivo, e ao segmento nulo está associado o número zero.
3.4. Axiomas sobre Medição de Ângulos
Analogamente ao caso de segmentos, introduziremos o conceito de medida de ângulo, o que também nos possibilitará compará-los em tamanho. Assim, Ângulo é uma figura geométrica formada por duas semi-rectas com mesma origem.
As semi-rectas são chamadas de lados do ângulo e a origem comum é o vértice do ângulo. Se os lados de um ângulo são semi-rectas opostas, esse ângulo é chamado de ângulo raso; caso os lados são semi-rectas coincidentes, chamamos o ângulo de ângulo nulo.
Existem várias formas de representar um ângulo. Por exemplo, se O é o vértice e A, B são pontos distintos de um ângulo, um em cada lado do ângulo, este pode ser representado por AOB\ ou BOA\.
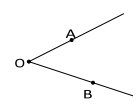
Ângulo AOB\.
Em algumas ocasiões, é comum utilizar letras minúsculas do alfabeto grego para representar um ângulo. Neste caso, é usual escrever a letra que designa o ângulo próximo do vértice e entre as duas semi-rectas.

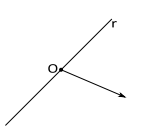
Dado um número real r> 0, é possível colocar em correspondência biunívoca os números reais entre 0 e r e as semi-retas de mesma origem que dividem um dado semi-plano. Aos ângulos rasos e nulos ficam associados os números r e zero, respectivamente, e reciprocamente. Divisão de um
semi-plano.
Ângulos consecutivos e adjacentes: Dois ângulos são chamados consecutivos se eles têm um lado em comum. Se os outros lados dos ângulos estão em semi-planos opostos, definidos pelo lado comum, esses são chamados adjacentes. Por exemplo: os ângulos AOB\ e AOC são consecutivos
e adjacentes; no entanto, AOB\ e BOC\ são consecutivos mas não são adjacentes.
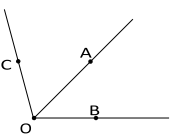
Dois ângulos são chamados suplementares se a soma de suas medidas é 180o. O suplemento de um ângulo é o ângulo adjacente ao ângulo dado obtido pelo prolongamento de um de seus.
Exemplo:
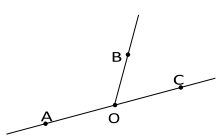
Ângulos opostos pelo vértice são aqueles em que os lados de um são as respectivas semi-retas opostas aos lados do outro. Exemplo
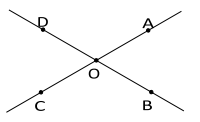
3.5.Axioma de congruência de triângulos
A noção de congruência é a de que dois segmentos ou ângulos congruentes têm a mesma medida.
Essa noção de congruência de segmentos e ângulos será naturalmente estendida aos triângulos, onde obteremos teoremas que nos dão condições suficientes para a congruência de triângulos. Dois triângulos são chamados de congruentes se existe uma correspondência biunívoca entre seus vértices de modo que lados e ângulos correspondentes sejam congruentes. Isso significa que se ABC e XY Z são dois triângulos congruentes e se Φ : {A,B,C} → {X,Y,Z}
Um triângulo que tem dois lados congruentes é chamado isósceles; os lados congruentes são as laterais e o terceiro lado é a base do triângulo. Um triângulo que tem os três lados congruentes chama-se equilátero.
O triângulo isósceles, os ângulos da base são congruentes. Demonstração. Seja ABC um triângulo isósceles, com AB ≡ AC
Dado um triângulo ABC, considere um ponto D sobre a reta determinada por B e C. Se D é ponto médio do segmento BC, o segmento AD chama-se mediana do triângulo ABC relativo ao vértice
A. Se D é tal que CAD\ ≡ DAB\, AD chama-se a bissectriz do ângulo AB. Se D é tal que a reta
AD é perpendicular à reta BC, AD é chamada altura do triângulo ABC relativo ao vértice A.
3.6.Axiomas das Paralelas
A consistência da geometria apresentada por Hilbert estabeleceu o quinto postulado de Euclides como um axioma, independente dos demais. Este axioma caracteriza o que hoje chamamos de Geometria Euclidiana Plana. Adotaremos aqui, como já mencionado, o enunciado devido a Playfair. Nesta forma equivalente, o axioma afirma a unicidade da reta passando por um ponto e paralela a uma reta dada.
Ângulos correspondente. Exemplo:
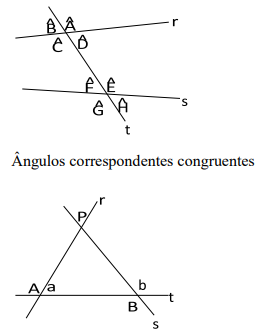
3.7. Axioma sobre Áreas
O conceito de área de regiões poligonais, que será feito mediante alguns axiomas, os quais permitirão introduzir as fórmulas usuais para a área de triângulos, rectângulos e demais polígonos. Como aplicações do conceito de área, veremos os famosos Teorema de Pitágoras e o Teorema de Tales.
Este número real igual a 1, associado a cada região unitária, é chamado de área da região unitária. Portanto, qualquer região unitária tem área igual a 1. Além disso, o número real obtido da comparação de uma figura geométrica F com a região unitária será chamado a área da figura F, e será denotado por Área (F).
A noção da área de regiões poligonais e introduzida na geometria através dos seguintes axiomas:
Axioma de toda região poligonal corresponde um número maior do que zero. O número a que se refere este axioma e chamado de área da região.
Axioma, Se uma região poligonal a união de duas ou mais regiões poligonais que duas a duas nãotenham pontos interiores em comum, então sua área e a soma das áreas daquelas regiões.
E claro que todo polígono convexo determina uma região poligonal. Nos iremos tomar a liberdade de usar expressões do tipo área de um quadrado” quando queremos dizer realente área da região poligonal cuja fronteira um quadrado”. Em geral falaremos de a\rea de um dado polígono”
Área (A BC D) = Área (A BC E) + Área (A DE) =
= Área (A BC E) + Área (C BF) =
= Área (A BF E) = b h
Conclusão
Tendo concluído a pesquisa, concluiu-se que A palavra “geometria” vem do grego geometrein (geo, “terra”, e metrein, “medida”); originalmente geometria era a ciência de medição da terra. O historiador Herodotus (século V a.C.), credita ao povo egípcio pelo início do estudo da geometria, porém outras civilizações antigas (babilônios, hindu e chineses) também possuiam
muito conhecimento da geometria.
A História da Geometria e da sua relação com outras áreas matemáticas, nomeadamente a Álgebra elementar, desde as origens heurísticas (egípcios e babilónicos), passando pelo desenvolvimento e sistematização durante o período helenístico (axiomática de Euclides) e cobrindo, a traços largos, desenvolvimentos posteriores (o problema das paralelas) até ao descobrimento das geometrias não-euclidianas no século XIX. Assim, existiram muitos filósofos a estudarem a Geometria na antiguidade, mas é sem dúvida com os geómetras gregos, começando com Táles de Mileto (c. 624--547 a.C.); Pitágoras (c. 572-497 a.C.); Arquimedes de Siracusa (c.
287 – 212); Euclides (330 a.C.), entre outros.Contudo Euclides é quem mas se destacou na geometria. Ele foi “O pai da Geometria” em Alexandria, como professor de matemática (geometria e álgebra).
Tudo o que sabemos sobre Euclides foi escrito muito depois de sua passagem pela Terra. Euclides pensava na geometria como um modelo abstrato do mundo. As ideias do ponto, linhas, formas foram derivadas do que foi visto no mundo real. Ele estudou objetos do mundo real para formalizar o conceito de sólido. E ele tem suas definições na Geometria.
No contexto dos axiomas observou-se que um axioma é um conceito matemático que não precisa de demonstração para ser verdadeiro. É uma ideia considerada óbvia e tomada como consenso, mesmo sem provas para tal. Os axiomas servem como base para a dedução de outras verdades. E
os axiomas têm vários como: Axioma de incidência; axioma de ordem; axioma de medição de segmentos; axiomas de medição de ângulos; axiomas paralelos; axiomas sobre áreas e entre outros. É indiscutível a importância e influência que a Matemática tem na vida das pessoas, principalmente, quando se trata de Geometria Euclidiana e Descritiva, visto estás estãopresentes em nosso cotidiano.
Referência bibliográfica
Barbosa, João. L. Marques, (2005).“Geometria Euclidiana plana”, SBM, 2005.
C. Gorodski, (2008). Um panorama histórico da Geometria, Matemática Universitária, SBM, 44, 14 – 29.
D. Hilbert, (1950). The Foundations of Geometry, the Open Court Publishing Company.
E. L. Lima, (1991). Medida e Forma em Geometria, Sociedade Brasileira de Matemática.
Greenberg, Martin J., (1993). “Euclidean and non-Euclidean geometries”, W. H. Freeman and company,
G. Ávila, Euclides, (2001). Geometria e Fundamentos, Revista do Professor de Matemática, SBM, 45.
H. S. M. Coxeter, (1967). Geometry Revisited, New Mathematical Library, The L. W. Singer Company.
João. L. M. Barbosa, (2006). Geometria Euclidiana Plana, Sociedade Brasileira de Matemática.
M. P. do Carmo, (1987). Geometrias não-Euclidianas, Matemática Universitária, SBM, 6, 25 –48.
P. C. P. Carvalho, (1993). Introdução à Geometria Espacial, Sociedade Brasileira de Matemática.
T. L. Heath, (1956). The Thirteen Books of Euclid’s Elements, Vol. 1e 2, Dover Publications.
Rezende, et al, (2004). Geometria Euclidiana plana e construções geométricas

